Diese Seite funktioniert nur mit Javascript.
Grenzrate der technischen Substitution3.2.6 Niveauproduktionsfunktion, SkalenerträgeMinimalkostenkombination
enn man alle Faktoreinsätze gleichermaßen variieren lässt, erhält man eine Niveauproduktionsfunktion oder Ertragskurve bei totaler Faktorvariation. Am einfachsten stellt man sich vor, dass die einzelnen Faktoren in einem Faktorpaket geschnürt werden und dann gemessen wird, wie hoch die Produktion in Abhängigkeit vom Einsatz solcher Faktorpakete ausfällt. Wenn weiterhin der 2-Faktoren-Fall mit Kapital $K$ und Arbeit $L$ als Produktionsfaktoren betrachtet wird, könnte z.B. $(K,L) = (2,1)$ als ein Faktorpaket vereinbart werden. $(K,L) = (10,5)$ bedeutete dann den Einsatz von 5, $(K,L) = (12, 6)$ den Einsatz von 6 Faktorpaketen. Die Kapitalintensität bleibt konstant, da sich die Zusammensetzung der einzelnen Pakete nicht ändert.
Die aus der Erhöhung des Faktorpaketeinsatzes um eine Einheit resultierende Produktionssteigerung heißt zur Unterscheidung vom Fall partieller Faktorvariation nun nicht mehr Grenz-, sondern (marginaler) Skalenertrag. An die Stelle der partiellen Produktionselastizität tritt die Skalenelastizität. Abbildung 1 zeigt eine Niveauproduktionsfunktion, die dem Verlauf des Klassischen Ertragsgesetzes folgt und in P eine Skalenelastizität von 1 besitzt.
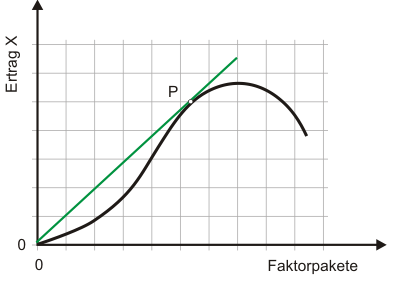
Wenn die Skalenelastizität über 1 liegt, spricht man von zunehmenden Skalenerträgen. Zunehmende Skalenerträge bedeuten sinkenden Faktorverbrauch pro Stück und somit sinkende Durchschnittskosten, da bei einer Skalenelastizität über 1 die Produktion relativ stärker ansteigt als der Faktoreinsatz.* In Abbildung 1 zeigt der Bereich 0P zunehmende Skalenerträge und zunehmende Durchschnittserträge, die sich jetzt natürlich - da Faktorpakete betrachtet werden - nur noch wertmäßig angeben lassen, da die Faktoren aggregiert werden müssen. In diesem Bereich sinken die Durchschnittskosten, d.h. der Gewinn wird steigen, wenn die Produktion ausgedehnt wird. Rechts von P sind abnehmende Skalenerträge zu beobachten.
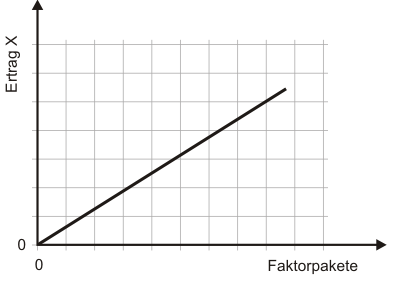
Wenn die Skalenelastizität einen Wert von 1 annimmt, spricht man von konstanten Skalenerträgen. Während sich beim klassischen Ertragsgesetz die Skalenelastizität laufend ändert, gibt es andere Produktionsfunktionen, bei denen die Skalenelastizität immer den gleichen Wert hat. Die Leontief-Produktionsfunktion ist ein Beispiel. Sie hat durchgängig eine Skalenelastizität von 1. Unabhängig vom Ausgangsniveau führt eine Ver-x-fachung der Inputs zu einer Ver-x-fachung des Outputs. Abbildung 2 macht deutlich, warum Produktionsfunktionen mit einer durchgängigen Skalenelastizität von 1 linear genannt werden.
Auch die Cobb-Douglas-Produktionsfunktion weist konstante Skalenerträge auf, wenn die partiellen Produktionselastizitäten der Faktoren sich auf 1 summieren. Um dies zu zeigen, wird für die Produktionsfunktion $x = c K^a L^b$ die Produktionsmenge berechnet, wenn der Einsatz beider Faktoren jeweils ver-$\lambda$-facht wird:
$$ q = c (\lambda K)^a (\lambda L)^b = c \lambda^a K^a \lambda^b L^b = \lambda^a \lambda^b c K^a L^b = \lambda^{a+b} x \tag{1}$$Wenn $a+b=1$ gilt, beträgt das Produktionsergebnis $q$ des $\lambda$-fachen Faktoreinsatzes das $\lambda$-fache des ursprünglichen Produktionsergebnisses $x$. Wenn also z.B. die Faktoreinsätze verdoppelt werden ($\lambda = 2$), so verdoppelt sich auch das Produktionsergebnis. Bei konstanten Skalenerträgen sind die Durchschnittskosten somit unabhängig vom Produktionsniveau, also konstant.
Die Elastizität $E_{q,\lambda}$ ist die Elastizität des Produktionsergebnisses $q$ bzgl. des Skalenniveaus $\lambda$, die Skalenelastizität. Wie im Abschnitt über Elastizitäten gezeigt, kann man in der Funktion $q = \lambda^{a+b} x$ die Elastizität $E_{q,\lambda}$ unmittelbar als $(a+b)$ ablesen. Gleichung (1) zeigt also für die Cobb-Douglas-Produktionsfunktion eine Skalenelastizität, die sich als Summe der partiellen Produktionselastizitäten ergibt.
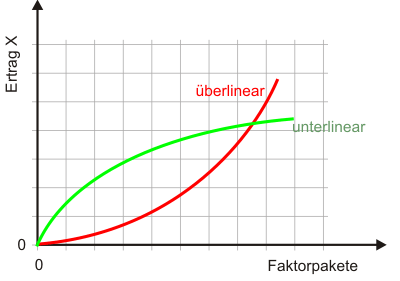
Produktionsfunktionen mit konstanter Skalenelastizität werden homogen genannt ( Homogenitätsgrad). Die Cobb-Douglas-Produktionsfunktion ist homogen vom Grad $(a+b)$. Wenn $a+b \gt 1$ gilt, nennt man die Produktionsfunktion überlinear homogen, wenn $a+b = 1$ linear homogen und andernfalls unterlinear homogen. Abbildung 3 zeigt eine über- und eine unterlinear homogene Niveauproduktionsfunktion, Abbildung 2 zeigt eine linear homogene Produktionsfunktion.
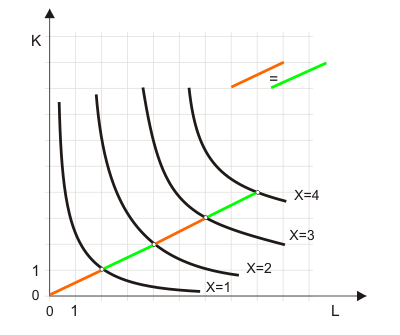
Ob eine Produktionsfunktion über- oder unterlinear homogen ist, kann man auch im Isoquantendiagramm erkennen. Wenn man wie in Abbildung 4 einen Strahl durch den Ursprung zeichnet (= konstante Kapitalintensität), müssen bei konstanten Skalenerträgen die Abstände zwischen den Isoquanten immer gleich bleiben, da unabhängig vom Ausgangsniveau gleiche Faktoreinsatzerhöhungen gleiche Outputzuwächse zur Folge haben müssen.
Gleichwohl spricht man in diesem Zusammenhang vom Gesetz abnehmender Ertragszuwächse. Folgende Plausibilitätsüberlegung spricht eher für konstante Skalenerträge: Wenn eine Unternehmung x Stück produziert, dann kann man mit zwei Unternehmungen 2 mal x Stück produzieren. Sicher finden sich sowohl Argumente, warum man mit zwei Unternehmungen auch mehr produzieren könnte als das Doppelte des Produktionsergebnisses einer Unternehmung, als auch solche, warum sich die Produktion weniger als verdoppelt. Aber in der Tendenz ist auf lange Sicht - also wenn alle Produktionsfaktoren variabel sind - eine Skalenelastizität von 1 zumindest nicht unplausibel. Und das würde bedeuten, dass langfristig eine Produktionsausweitung zu konstanten Stückkosten möglich ist.
Nach ähnlichen Seiten im WWW suchen